SIMPLE INTRODUCTION TO MUNBER THEORY

1. Meet the Munbers!

1.1 Definition and properties of munbers

A munber is a unique entity that has no parallel in all of mathematics. People often mistakenly find munbers to be equivalent to sets, although this is not the case.

DEFINITION. If a₁, a₂, ... a_n are real numbers, the object «a₁, a₂, ... a_n» is called a real munber.

The difference between this and a set is that although each are comprised of a certain group of elements, more operations can be performed upon munbers than on sets. Thus, munbers occupy the "netherworld" between numbers and sets.

DEFINITION. Let a ≡ «a₁, a₂, ... a_n» be a real munber and b be a real number. Then we say a is equal to b [a = b] iff ∃ k ∈ Z⁺, k ≤ n, st a_k = b.

In other words, munber a = number b if and only if b is a member of a. Similarly, we can now begin to discuss equality between munbers themselves.

DEFINITION. Let a ≡ «a₁, a₂, ... a_m» and b ≡ «b₁, b₂, ... b_n» be real munbers. Then we say a is equal to b [a = b] iff ∃ j,k ∈ Z⁺, j ≤ m and k ≤ n, st a_j = b_k.

In other words, munber a = munber b if and only if they share at least one common member. Note that sometimes it is easier to refer to numbers as being members of munbers, just as we speak of elements of sets. This means that a number is a member of a munber if that number is equal to the munber. Of course, it is not enough to say this much about munbers, since two munbers may be equal to one another without being the same munber.

DEFINITION. Let a ≡ «a₁, a₂, ... a_m» and b ≡ «b₁, b₂, ... b_n» be real munbers. Then we say a is part of b [a ⊆ b] iff ∀ j ∈ Z⁺, j ≤ m, ∃ k ∈ Z⁺, k ≤ n, st a_j = b_k.

This means that a is part of b if and only if all members of a are also members of b. It may plainly be seen that if the reverse is also true, the munbers are identical.

DEFINITION. Let a and b be real munbers. Then we say a is identical to b [a ≡ b] iff a ⊆ b and b ⊆ a.

Thus it is clear that two munbers may be equal without being identical. Herein lies the power of munbers, as we shall see. Also, note that a munber may be identical to a number: munber a ≡ number b if and only if a ≡ «b». In particular, this shows that numbers are themselves munbers that happen to have one member. Other important observations on munbers are that, as with sets, order and duplicity are trivial, ie, «1, 2, 3» ≡ «1, 3, 2» ≡ «1, 2, 3, 3».

1.2 Operations on munbers

Any mathematical concept worth its salt will provide a means of adding and multiplying them. Here's how we do this to munbers.

DEFINITION. Let a ≡ «a₁, a₂, ... a_m» and b ≡ «b₁, b₂, ... b_n» be real munbers. Then the sum of a and b [a + b] is identical to «a₁ + b₁, a₁ + b₂, ... a₁ + b_n, a₂ + b₁, a₂ + b₂, ... a₂ + b_n, ... a_m + b₁, a_m + b₂, ... a_m + b_n».

To obtain the sum of two munbers, one simply sums each member of the first munber with each member of the second munber and puts all these numbers into the result. Defining multiplication of munbers, however, takes some work. First we must consider "scalar multiplication" of munbers, ie, how we multiply munbers by numbers. Obviously, the product of a munber and a number must be equal to the result of adding the munber to itself that many times. Any munber added to itself is clearly equal to twice each member, added to itself three times is equal to three times each member, and so on. This motivates the following definition.

DEFINITION. Let a ≡ «a₁, a₂, ... a_m» be a real munber and b be a real number. Then the product of a and b [a × b, a · b, or ab] is identical to «a₁b, a₂b, ... a_mb».

Now it is clear that we can do this with each member of a second munber and combine the results to yield the product of those munbers. First, though, we require another definition, again borrowed from set theory.

DEFINITION. Let a ≡ «a₁, a₂, ... a_m» and b ≡ «b₁, b₂, ... b_n» be real munbers. Then the union of a and b [a ∪ b] is identical to «a₁, a₂, ... a_m, b₁, b₂, ... b_n».

Using this definition, we can claim that the product of two munbers is the union of the products of one munber with each member of the other munber, or more generally:

DEFINITION. Let a ≡ «a₁, a₂, ... a_m» and b ≡ «b₁, b₂, ... b_n» be real munbers. Then the product of a and b [a × b, a · b, or ab] is identical to «a₁b₁, a₁b₂, ... a₁b_n, a₂b₁, a₂b₂, ... a₂b_n, ... a_mb₁, a_mb₂, ... a_mb_n».

To round out our group of definitions, let us add one more set-related definition.

DEFINITION. Let a and b be real munbers. Then the intersection of a and b [a ∩ b] contains a real number x iff x = a and x = b.

In this way, we can back up and say that a ∪ b contains x if and only if x = a or x = b.

DEFINITION. Let a and b be real munbers. Then a and b are said to be disjoint iff there does not exist a real number x st x = a and x = b. In this case, we take a ∩ b to be undefined.

Note another divergence from set theory; the intersection of disjoint sets is the empty set ∅, but the intersection of disjoint munbers has no value; there is no "empty munber".

1.3 Field properties of munbers

THEOREM 1.1. The operations of addition and multiplication of real munbers satisfy the commutative, associative, and distributive laws. In particular, if a, b, and c are arbitrary real munbers, we have the following:

• Commutative laws: a + b = b + a, ab = ba.
• Associative laws: a + (b + c) = (a + b) + c, a(bc) = (ab)c.
• Distributive laws: a (b + c) = ab + ac.

Proof. Each of these laws is painfully obvious from the sum and product definitions. Indeed, these must be not only equal, but identical to one another. The theorem uses equality simply to fit in with the first three field axioms. It is left to the reader to prove these, as it is reasonably straightforward.

This theorem plainly shows us that the set of all real munbers, which we will denote as M_R, satisfies the first three field axioms, so let us move on to the next three field axioms. Axiom 4 states that there are additive and multiplicative identities. As one can see, for a real munber a, a + «0» = a and «1»a = a. Axiom 5, which demands negatives, may be satisfied by observing that a + -1 · a = «0»; we will write -a for -1 · a and call it the negative of a. In the case of Axiom 6, given a real munber a ≠ 0, we can construct another real munber, b, containing only those numbers that are reciprocals of the members of a. Then, we see that ab = 1 as required. This b is the reciprocal of the munber a and is symbolized a^-1.

The astute observer will notice that the above cases are not the only ways to satisfy these three axioms. For example, «4, 8» «2, 4» ≡ «8, 16, 32» = «4, 8». Thus, «2, 4» is a multiplicative identity for «4, 8», but it is not the only multiplicative identity. Other chance arrangements like this will yield additional solutions to Axioms 4 through 6, motivating us for another theorem.

THEOREM 1.2. ∀ a, b, c ∈ M_R, if b = 0 and c = 1, then a + b = ac = a.

Proof. If b = 0, then a + b will include, at the least, all members of a, implying that a + b = a. Similarly, if c = 1, then ac also includes all members of a and is also equal to a. This completes the proof.

THEOREM 1.3. ∀ a, b ∈ M_R, a + b = 0 iff a = -b.

Proof. A munber that is equal to zero merely has that as a member, so there must be some combination of members of a and b, say a_m and b_n, the sum of which is zero. Thus a_m = -b_n and by the definition of equality of munbers, a = -b. The converse is proven likewise, only in reverse.

THEOREM 1.4. ∀ a, b ∈ M_R, ab = 1 iff a = b^-1.

Proof. As above, there must be some combination of members of a and b, say a_m and b_n, the product of which is one. Thus a_m = b_n^-1, implying that a = b^-1. We can reverse the steps in order to prove the converse.

Some theorems that hold for real numbers fail miserably in the case of real munbers if one forgets that equality for real munbers is not the same as identicality. For arbitrary real munbers a, b, c, and d, these theorems are true:

THEOREM 1.5. CANCELLATION LAWS. If b = c, then a + b = a + c and ab = ac.

THEOREM 1.6. POSSIBILITIES OF SUBTRACTION AND DIVISION. If a + c = b and a + d = b, then c = d = b + (-a), which may also be written as b - a. Namely, 0 - a ≡ -a. If a ≠ 0, ac = b and ad = b, then c = d = b · a^-1, which may also be written as b/a. Namely, 1/a ≡ a^-1.

THEOREM 1.7. -(-a) ≡ a, a(b - c) ≡ ab - ac, 0 · a ≡ a · 0 ≡ 0, (-a)b ≡ -(ab), and (-a)(-b) ≡ ab.

THEOREM 1.8. If a ≠ 0, then b/a ≡ b · a^-1 and (a^-1)^-1 ≡ a.

THEOREM 1.9. If ab = 0, then a = 0 or b = 0. If ab ≡ 0, then a ≡ 0 or b ≡ 0.

THEOREM 1.10. If b ≠ 0 and d ≠ 0, then (a/b) + (c/d) = (ad + bc)/(bd) and (a/b)(c/d) ≡ (ac)/(bd). Furthermore, if c ≠ 0 as well, then (a/b)/(c/d) ≡ (ad)/(bc).

Since the six field axioms are satisfied, M_R is a field, but clearly a completely different field than R. Facts that we take for granted in real numbers, such as the uniqueness of 0, are not true for real munbers. But a more important fact is that while 0 is not unique in the set of real munbers, all munbers that serve as zero elements are equal to one another, as we proved in Theorem 1.2. We again caution the reader that with munbers, equality is not synonymous with identicality. At first, this causes merely migraines for munber students, but once these concepts are mastered, the apprentice is ready to appreciate all that may be done with these remarkable tools.

1.4 Exercises

1. Express the following sets of numbers as munbers.
   

   (a) {0, 1, 2, 3}	(c) {12 - 3, 4 + 5}
   (b) {π} ∪ {0, π, 2π}	(d) Z+

2. In each case, determine whether the first munber is identical to, part of, equal to, or unequal to the second.
   

   (a) «-2, 2, 5», «-8, -2, -1»	(d) «2, 3», «all numbers found on a fair die»
   (b) «-2, 2», «all solutions x of x² = 4»	(e) «e0, e1, e2, ... », «all positive integers»
   (c) «-2, 0, 2», «all solutions x of x² = 4»	(f) «0, ± x», «0, ± y», where x ≠ y

3. In each case, determine the sum and the product of the given munbers.
   

   (a) «-2, 2, 5», «-8, -2, -1»	(e) «0, 1, 2, 3», «-2, -1»
   (b) «-2, 2», «all solutions x of x² = 4»	(f) «0, ± x», «0, ± y», where x ≠ y
   (c) «-2, 0, 2», «all solutions x of x² = 4»	(g) «4000, 8000, 12000», «.04, .08»
   (d) «π», «2π»	(h) «-5, 0, 1», «-5, 0, 1»

4. Repeat Exercise 3, but subtract the second munber from the first.
5. Repeat Exercise 3 once more, but divide the first munber by the second.
6. Let m and n be integer munbers; that is, they consist entirely of integers.
   (a) Show that m + n and mn are also integer munbers.
   (b) For both m - n and m/n, either show that it is an integer munber or specify what must be true in order for that value to be an integer munber.
7. For arbitrary munbers a and b, prove the converse of Theorem 1.9. That is, prove that a = 0 or b = 0 implies that ab = 0, and that a ≡ 0 or b ≡ 0 implies that ab ≡ 0.
8. In some systems, such as in the real numbers, we may define ordering that satisfies the following three axioms.

   AXIOM 7. If x and y are in R⁺, so are x + y and xy.

   AXIOM 8. ∀ x ≠ 0, either x ∈ R⁺ or -x ∈ R⁺, but not both.

   AXIOM 9. 0 ∉ R⁺.

   (a) Prove that no ordering system for munbers can satisfy Axioms 7, 8, and 9 simultaneously.
   (b) Formulate an ordering system that satisfies Axioms 7 and 9, but not Axiom 8. If none exists, show why.
   (c) Formulate an ordering system that satisfies Axioms 8 and 9, but not Axiom 7. If none exists, show why.
9. Let a be a munber with x members, and let b be a munber with y members. What is the minimum number of members that ab may have?

1.5 Geometric representation of munbers

The most immediately apparent way to represent a munber would be to utilize the number line, placing a point upon each number that is a member of the munber as in Figure 1.1. Multiple munbers may be shown either on separate "munber lines" or with different symbols on the same munber line. As depicted in Figure 1.2, either method is well suited to the set interpretation of munbers by immediately displaying the intersection and the union of munbers. Using this method, we find that it is easy to see when munbers have certain properties.

DEFINITION. Let a be a real munber. Then a is said to be symmetric about zero iff a ≡ -a.

In particular, this definition tells us that for every real number x = a, -x = a as well. Graphing such a munber shows us immediately why we say that it is "symmetric", as the example in Figure 1.3 shows. Obviously, there is no need to constrain ourselves to munbers symmetric about zero.

DEFINITION. Let a be a real munber and let x be a real number. Then a is said to be symmetric about x iff a - x ≡ -(a - x). In addition, we call x the axis of symmetry for a.

Symmetry for munbers is analogous to symmetry of a one dimensional figure, and like a one dimensional figure, there may only be one axis of symmetry for a finite munber.

THEOREM 1.11. Let a be a real munber with a finite number of members. If a is symmetric about the real number x, it is not symmetric about any other real number; ie, a real munber may have at most one axis of symmetry.

Proof. Using the definition of symmetry, we shall prove that if a munber is symmetric about two numbers, those numbers are equal. Suppose that a is symmetric about both x and y. By definition, this means that a - x ≡ -(a - x) and a - y ≡ -(a - y). Using Theorem 1.6, we rewrite this as a ≡ -(a - x) + x ≡ -a + 2x and a ≡ -(a - y) + y ≡ -a + 2y. Thus, -a + 2x ≡ -a + 2y. Using Theorem 1.5 and dividing by two, we have x = y, which we set out to prove.

As we saw in the last set of Exercises, there is no way to define positive and negative for munbers such that every munber other than 0 falls into either of these classes. We can, however, use an intuitive definition that, while weak, still has some redeeming qualities.

DEFINITION. Let a ≡ «a₁, a₂, ... a_n» be a real munber. Then we say a is positive iff ∀ k ∈ Z⁺, k ≤ n, a_k > 0.

A real munber is negative if all its members are negative, or alternatively, if its negative is positive. This is another property that has a fairly simple graphical representation. Proofs that sums, products, and quotients of positive munbers are positive are left to the reader, as they aren't hard at all.

1.6 Using geometric representations

There is a simple way to add munbers using the munber line method, outlined in Figure 1.4. Let two real munbers, a and b, be plotted on munber lines. The plot of b is rotated 90° and is superimposed on the plot of a such that the zero points coincide. Then, we have a set of ordered pairs (a_j, b_k), each of which corresponds to a member of the result. The sum comprises each of the sums of the values in each ordered pair. To graphically represent this, lines with slopes of -1 may be drawn, and each point traced along the line it intersects until it crosses either axis. The sum is the munber containing each resulting point.

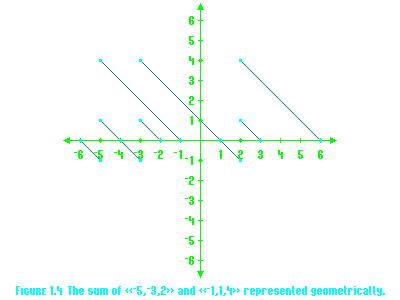
The method for multiplying two munbers is not as straightforward but is similar. We use the munbers' plots as axes again, plotting all points of intersection. Then, the product of each point is taken and placed in our answer. Other functions of munbers can also be taken from this munber line representation.

DEFINITION. Let a ≡ «a₁, a₂, ... a_n» be a real munber. Then we say n is the degree of a, symbolized n = deg(a).

Armed with all of these properties of munbers, we are now ready to put these tools to use. In the following chapters, we shall see how to use munbers as though they were numbers or as though they were sets.

1.7 Exercises

1. In each case, illustrate the given munber on a munber line, and specify its axis of symmetry, if any.
   

   (a) «-2, 2, 5»	(d) «all numbers found on a fair die»
   (b) «all solutions x of x² = 4»	(e) «e0, e1, e2, ... »
   (c) «-2, 0, 2»	(f) «0, ± x, ± y», where x ≠ y

2. In each case, use munber lines to add the given munbers.
   

   (a) «-1, 0, 3», «-8, -7, -6»	(e) «0, 1, 2, 3», «-8, -1»
   (b) «-1, 6», «all solutions x of x² = 4»	(f) «0, x, x²», «0, x, x²», where x ≠ y
   (c) «-1, 1, 6», «all solutions x of x² = 4»	(g) «0, ±2 · 105, 3 · 105, 4 · 106», «.01, .05»
   (d) «π», «π/2»	(h) «0, 3, 8», «0, 3, 8»

3. Repeat Exercise 2, but subtract the second munber from the first with munber lines.
4. Repeat Exercise 2 once more, but multiply the two munbers with munber lines.
5. Let a and b be real munbers; a is symmetric about x, and b is symmetric about y.
   (a) About what points are a + b and a - b symmetric, if any?
   (b) About what point is ab symmetric, if any?
6. Let a and b be real munbers, each of degree d.
   (a) Find the degree of a - b if there are no duplicates; that is, a_j - b_k = a_m - b_n implies that j = m and k = n.
   (b) Find the degree of a ∩ b in terms of x, the number of members that a and b share.
   (c) Find the degree of a ∪ b in terms of x.