SIMPLE INTRODUCTION TO MUNBER THEORY

3. Munbers as Numbers

3.1 Introduction

Without a doubt, the most useful mathematical construct ever designed has been the numbers. Whether real or complex, the numbers are the fundamental basis of mathematics as we know it. Almost any problem may be solved with numbers if one is sufficiently adept at their use; such is the entire purpose of mathematics itself. At the same time, mathematics is also intended to formulate new ways to solve problems that are easier than numbers in certain cases. First there were sets, then functions, then vectors, and now there are munbers. I fully expect to see munbers adopted into the standard toolbox of mathematicians, just as we have seen with the other devices that I just listed. One thing that helps these is if they may be treated in ways similar to the way numbers are treated. This is perfectly logical, since everyone knows how to use numbers. Although not everyone knows how to use munbers [for that matter, I'm not sure as to the definitive way to use them], I hope that I can explain their use in terms of numbers. So here goes.

NOTE. Throughout this chapter, I refer to "numbers" and "munbers" in a general sense. By this I mean numbers in any field F, and the corresponding munbers in M_F. In certain cases within this chapter, I will refer to F and G for the sake of simplicity; F and G may be any field, most commonly R and C, the sets of real and complex numbers. In particular, they may be, and frequently are, the same field.

3.2 Binary operations on munbers

We've already defined addition, subtraction, multiplication, and division in terms of munbers. The one common thread between these various operations has been that to pull them off, we simply take all possible combinations of member numbers and throw their sums, differences, products, or quotients into the result. So, why don't we generalize this?

DEFINITION. Let ¤ : F² → G be a binary operation. If a ≡ «a₁, a₂, ... a_n», b ≡ «b₁, b₂, ... b_n» ∈ M_F, then the value of a ¤ b is defined to be identical to «a₁ ¤ b₁, a₁ ¤ b₂, ... a₁ ¤ b_n, a₂ ¤ b₁, a₂ ¤ b₂, ... a₂ ¤ b_n, ... a_m ¤ b₁, a_m ¤ b₂, ... a_m ¤ b_n».

There is now some way to do anything at all between two munbers. All that is necessary is to determine the magic operator that takes in two numbers and outputs another number. Then, it may be used on two munbers to the same effect. The reader may verify that when this process is used upon munbers of degree one, the result is also a munber of degree one, thereby ensuring that degree-one munbers continue to behave the same as numbers.

THEOREM 3.1. If binary operations on numbers satisfy the commutative, associative, and distributive laws, then the analogous binary operations on munbers also satisfy the same laws. In particular, if a, b, and c are arbitrary munbers on F, x, y, and z are arbitrary numbers in F, and ¤ and # are arbitrary binary operations, we have the following:

• Commutative laws: If x ¤ y = y ¤ x, then a ¤ b ≡ b ¤ a.
• Associative laws: If x ¤ (y ¤ z) = (x ¤ y) ¤ z, then a ¤ (b ¤ c) ≡ (a ¤ b) ¤ c.
• Distributive laws: If x ¤ (y # z) = (x ¤ y) # (x ¤ z), then a ¤ (b # c) ≡ (a ¤ b) # (a ¤ c).

Proof. This proof will be left as an exercise for this chapter.

3.3 Functions of munbers

We commonly do one of two things to numbers: binary operations and functions. Having covered binary operations, let's proceed to functions. We have already addressed some functions that may be performed upon munbers, including scalar multiplication. It is logical that this not be a special function in any manner, which is why functions of munbers may be defined as follows.

DEFINITION. Let f : F → G be a unary function. If a ≡ «a₁, a₂, ... a_n» is a munber on F, then the value of f(a) is defined to be identical to «f(a₁), f(a₂), ... f(a_n)».

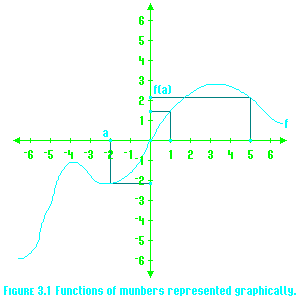
Graphically, it's remarkably easy to do this given only the graph of a function. [See Figure 3.1.] Some functions have rather interesting uses when applied to munbers, as shown in the following examples.

EXAMPLE 1. Let f(x) = x^-1. In this case, f(a) for some munber a is equal to its reciprocal, mentioned in Chapter 1. A natural reaction is to ask what happens when a = 0. If that is so, then f(a) obviously cannot be equal to ∞. Since the reciprocal of 0 is not a number, it cannot be equal to a munber, so that value must be left out of the munber.

EXAMPLE 2. Let f(x) = 0. This is the zero function. When applied to munbers, it is easily seen that it again yields 0, or, to be more precise, «0». This again reminds the reader that the two are identical.

EXAMPLE 3. Let f(x) = sqrt(x). The square root function has two problems. The first is that all nonzero numbers have two square roots, one positive and the other negative. The second is that negative numbers have no real square roots. One of these problems was solved with the advent of complex numbers, which allow the square roots of -1 to be symbolized as ±i. A temporary solution to the first problem has existed for hundreds of years, with the "principal square root", which gives sqrt(x) a unique value by excluding it to nonnegative numbers. That, however, was not a satisfactory solution, and here is why.

3.4 Muneric inverses of functions

DEFINITION. Let a ∈ M_F be a munber, f : F → G be a function, and x ∈ G be a number. Then a is the muneric inverse of f at x iff ∀ z ∈ F, z = a iff f(z) = x.

We can obtain a muneric inverse for any function and any value of x, so we can combine all of these values for a given function into a completely new function; in this case, it actually is completely new.

DEFINITION. Let g : G → M_F and f : F → G be functions. Then g is the muneric inverse of f iff ∀ x ∈ G, g(x) is identical to the muneric inverse of f at z. Then we write g ≡ f^-1.

This is actually much more revolutionary than it seems: it is our first function that maps a number to a munber. Many functions can map a number to a munber, many more can map a munber to a number, and still more can map a munber to another munber. The functions of numbers with which we have worked in this chapter are such an example, but there are others that may not behave in the same manner.

3.5 Zero and unit munbers

The zero munber is exactly what its name implies: «0». It is clear that adding «0» to any munber returns a munber identical to the original, but it should also be noted that in order for the sum to be equal to the original, it suffices for the second addend to be equal to 0. In other words, a + b = a if b = 0. This result is from Theorem 1.2. In addition, it may also be seen that a + 0 ≡ a.

Similarly, the unit munber is «1» and is defined as that munber a such that ∀ b ∈ M_F, ab ≡ b. Once again, multiplying by a munber equal to one gives a munber equal to the original.

THEOREM 3.2. UNIQUENESS OF THE ZERO AND UNIT MUNBERS. Each field M_F has exactly one zero munber and exactly one unit munber.

Proof. We note that Theorem 1.5 would help us immensely if its statements were about identicality instead of equality. Thus, we will rewrite the cancellation laws and prove the modified form.

LEMMA 3.3. STRONG FORM OF CANCELLATION LAWS. For arbitrary a, b, c ∈ M_F, if a + b ≡ a + c, then b ≡ c. If a ≠ 0 and ab ≡ ac, then b ≡ c.

Proof. Let a', b', and c' be arbitrary member numbers of a, b, and c respectively. ∀ a' and b', ∃ a certain c' such that a' + b' = a' + c' by the definition of identicality. Using the cancellation laws for numbers, b' = c'. This shows that b ⊆ c. By commutativity, b and c may be reversed in the above steps to show that c ⊆ b and therefore that b ≡ c. To prove the second part, we do the same but obtain that a'b' = a'c'. From then on, the proof proceeds in the same manner.

Proof of Theorem 3.2. Suppose that F has two zero munbers, s and t. Then ∀ a ∈ M_F, a ≡ a + s ≡ a + t. Therefore by Lemma 3.3, s ≡ t. If F has two unit munbers j and k, then ∀ a ∈ M_F, a ≡ aj ≡ ak. Lemma 3.3 then implies that j ≡ k to complete the proof.

3.6 Exercises

1. For x, y ∈ R, define {x, y} = x + yi and x Þ y = y² - x. Find each of the following.
   

   (a) {2, 3}	(d) {π, (4 · 9) Þ 6}
   (b) 2(-1 Þ 1)	(e) {1/sqrt(2), ½}
   (c) {0 Þ 4, 4 Þ 0}	(f) (2 Þ 3) + (-2 Þ -3)

2. Use the definitions of {x, y} and x Þ y from Exercise 1. If a ≡ «2, 7», b ≡ «-3, -2, -1», and c ≡ «-10, 2, 10», find each of the following.
   

   (a) {a, c}	(e) {c, c}
   (b) b Þ b	(f) {a + 2, 3c}
   (c) {a - b, a}	(g) (a Þ b) - c
   (d) {a Þ a, a Þ -a}	(h) (a Þ a) ÷ (a Þ a)

3. Repeat Exercise 2, replacing a with -a, b with -b, and c with c^-1.
4. Using the values of a, b, and c from Exercise 2, find each of the following.
   

   (a) ln a	(e) ec + 1
   (b) b · b	(f) sqrt(-c)
   (c) b²	(g) -sqrt(c)
   (d) a!	(h) cos(bπ/2)

5. Using the results of the previous exercise, answer the following questions for an arbitrary munber a.
   (a) Must a · a ≡ a²?
   (b) Must a + a ≡ 2a?
   (c) If not, replace ≡ with =, ⊆, or ⊇.
6. Find the muneric inverses of the following functions of x at the given values. The relevant field is C.
   

   (a) x³, 64	(d) ln x, 0
   (b) x + sin x, π	(e) sqrt(-x), i
   (c) x + 1/x, 2.5	(f) -sqrt(x), i

7. Give a proof for Theorem 3.1.
8. Given a polynomial p(x), let p^-1(x) be its muneric inverse and p_M be its muneric root. Express the one in terms of the other, ie, produce a simple relationship between the two.
9. Suppose that in M_R, we change the definition of multiplication such that the new result is identical to half of the original product. In that case, do the zero and unit munbers exist? If so, what are they? If the definition of addition is changed such that the new sum is identical to the negative of the original, are there still zero and unit munbers, and if they exist, what are they?