


SIMPLE INTRODUCTION TO MUNBER THEORY
5.1 The need for weighted munbers
An astute reader has surely noticed a series of gaps in our development of munbers thus far. For example, the definition of nonoverlapping sums from the previous chapter is a haphazard way of getting around the fact that a number can only appear in a munber once. Exercise 6 in Section 4.7 showed us how valuable muneric frequencies can be. By exploring this concept in further detail, we shall see the true value of muneric frequencies.
To create a weighted munber, we assign a value to each member specifying its frequency.
DEFINITION. Let a be a munber on F. If each member ak of a has an associated real number wk, then we call each wk the weight of ak, and we write a ≡ «[w1] a1, [w2] a2, ... [wn] an».
DEFINITION. For a given value of x, the function Wa(x) returns the weight of x in the munber a.
Note that Wa(x) = 0 if and only if x ≠ a. Having defined these weights, it is now time to do something with them. Obviously, first we'll want to redefine the degree.
DEFINITION. The degree of the munber a defined above, written deg(a), is defined as ∑ wk.
The weight of a member number of a munber is the amount by which it counts. Until now, we have been working under the implicit assumption that all munbers have unitary weight for all members. This required quite a bit of twisting and wrangling to ensure that it is always true. But free from that requirement, munber theory can make great strides.
Let us go back and review our most basic definitions, this time from the standpoint of weighted munbers.
DEFINITION. Two munbers a and b are equal [a = b] iff ∃ some number x such that Wa(x) ≠ 0 and Wb(x) ≠ 0. a and b are identical [a ≡ b] iff Wa(x) = Wb(x) ∀ x.
Perhaps the largest adjustment that must be made in our redefinition of these terms is that identicality no longer requires only that the munbers have the same members. Now we must also check that they are weighted in the same manner.
DEFINITION. A munber a is positively weighted iff Wa(x) ≥ 0 ∀ x.
In our definition of the intersection, we specified that if two munbers are unequal, they are disjoint, and their intersection is undefined. We took that to mean that there is no munber with degree zero. However, using our weighted munbers, we see that we can construct a meaningful degree zero munber, such as «[-1] 0, 1». [If a member number of a munber has weight 1, we will often leave the weighting value out.] Note that negative weights are permitted. At this point our only restriction on weights is that they be real, but in future we may wish to explore complex weights.
Nonetheless, we consider a munber such that Wa(x) = 0 for all x. This would be the empty munber, and the intersection of disjoint munbers would return this munber. Since nothing can be done with the empty munber anyway, we shall continue to say that the intersection of unequal munbers is not defined, but we might sometimes express an undefined intersection as ∅.
DEFINITION. The intersection of two munbers a and b [a ∩ b] is the munber c such that ∀ x, Wc(x) is the closest member to zero of the interval [Wa(x), Wb(x)]. The union of a and b [a ∪ b] is the munber c such that ∀ x, Wc(x) = Wa(x) + Wb(x).
The intersection requires a bit of explaining. If both weights for a number are positive, that number's weight in the intersection will be the lesser of the two. If both weights are negative, the resulting weight will be the greater of the two. If the weights are of opposite sign, or if one of them is zero, the resulting weight will be zero. In short, the resulting weight will be as close to zero as it can get. From the union redefinition, a Union Degree Theorem immediately follows.
THEOREM 5.1. UNION DEGREE THEOREM. Let a and b be munbers of finite degree. Then deg(a ∪ b) = deg(a) + deg(b).
Proof. This is a direct consequence of the union definition.
DEFINITION. A munber a is part of a munber b [a ⊆ b] iff Wa(x) ≤ Wb(x) ∀ x.
With this definition as well as the original definition, two munbers are identical if and only if they are part of one another.
Another concept that needs redefinition is our treatment of binary operators from Chapter 3. Let's reexamine the addition of munbers. When you take two members of munbers, their sum will be a member of the resulting munber. That member's weight will be the product of the weights of the original members.
DEFINITION. Let a ≡ «[w1] a1, [w2] a2, ... [wm] am» and b ≡ «[v1] b1, [v2] b2, ... [vn] bn» be munbers on F. Then the sum of a and b is defined as a + b ≡ «[w1v1] a1 + b1, [w1v2] a1 + b2, ... [w1vn] a1 + bn, [w2v1] a2 + b1, [w2v2] a2 + b2, ... [w2vn] a2 + bn, ... [wmv1] am + b1, [wmv2] am + b2, ... [wmvn] am + bn».
Subtraction, multiplication, and division are defined in the same way. Sometimes, these computations overlap. When two different pairs of members produce the same sum, the obtained weighting values are summed, as one might expect. This gives us a clear way to find the degree of a muneric sum or product.
THEOREM 5.2. BINARY DEGREE THEOREM. Let a and b be munbers of finite degree. Then deg(a + b) = deg(a - b) = deg(ab) = deg(a/b) = deg(a)deg(b).
Proof. The degree of any of these is w1v1 + w1v2 + ··· + w1vn + w2v1 + w2v2 + ··· + w2vn + ··· + wmv1 + wmv2 + ··· + wmvn = w1(v1 + ··· + vn) + ··· + wm(v1 + ··· + vn) = (w1 + ··· + wm)(v1 + ··· + vn) = deg(a)deg(b).
COROLLARY 5.3. CONSERVATION OF UNITARY DEGREE. If munbers a and b both have degree one, then the values a + b, a - b, ab, and a/b also have degree one.
As we shall see, this property will become very useful in the realm of probability.
| (a) «[2] -2, 5», «-8, -2, -1» | (c) the muneric root of x² - 4, «[2] -2, 2» |
| (b) the muneric root of x² - 4, «-2, 2» | (d) «[4] 2, 3», «2, [4] 3» |
5.5 Applications of weighted munbers
In Chapter 2, we defined the concept of a muneric root. We saw that the muneric root had a degree that is no greater than the polynomial's degree. But if we utilize weighted munbers, we can say that the weights of each member of the muneric root are the same as the frequencies of that root. In this way we obtain a more rigid result.
THEOREM 5.4. The degree of a muneric root is equal to the degree of its polynomial.
Proof. This theorem is extremely obvious in light of weighted munbers.
EXAMPLE 1. The polynomial x² - 4 has roots 2 and -2, so its muneric root is «-2, 2». Its degree is clearly 2.
EXAMPLE 2. The polynomial x³ - 4x² + 4x has roots 0, 2, and 2, so its muneric root is «0, [2] 2». Its degree is 3. [We could also write the muneric root as «0, 2, 2».]
A muneric root, then, can define a polynomial to within a normalization constant. This leads us to consideration of muneric roots of a characteristic equation. Hence we have the muneric equivalent of the eigenvalues of a matrix or of an operator. To connect these eigenvalues to their associated eigenvectors, we might want to define muneric equivalents of vectors [cevtors?].
Another application of weighted munbers is in probability. The munber d ≡ «1, 2, 3, 4, 5, 6» represents the values on each face of a fair die. Then d + d represents the possible sums obtained when rolling a pair of dice. A bit of computation shows that d + d ≡ «2, [2] 3, [3] 4, [4] 5, [5] 6, [6] 7, [5] 8, [4] 9, [3] 10, [2] 11, 12», as we would expect.
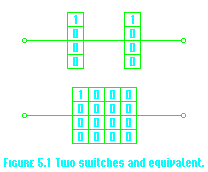
EXAMPLE 3. A circuit has two switches, each with four possible positions. [See Figure 5.1.] Current will flow through either switch only if that switch is in the first position. We can represent the possible positions of each switch as s ≡ «[3] 0, 1», where 0 means current is not passed and 1 means current is passed. To see whether current flows through the entire circuit, we take the product ss ≡ «[15] 0, 1». Since deg(ss) = 16, there are sixteen possible arrangements of the two switches. Current is passed in only one of these arrangements.
5.6 Interpretations of weighted munbers
There are two ways to explicitly describe a munber. The first is the «» notation that we have been using to this point. But a second method exists, one that we have been using but not acknowledging. Equality, identicality, and other properties have been defined in terms of weights of members, and it turns out that this is enough to define a munber itself.
Sometimes we will want to describe a munber by giving the closed form of its weighting function W(x). So far, we have been describing only munbers with discrete members, like «1, 2, 4». In the next chapter, though, we shall consider munbers with continuous members and examine their implications.
By now we have noticed something that munbers have in common with pigs: Munbers can be equal, but some munbers are more equal than others. To find out how equal two munbers are, we need look no further than their intersection.
THEOREM 5.5. CAUCHY-SCHWARZ INEQUALITY FOR MUNBERS. Suppose munbers a and b are both positively weighted. Then deg(a ∩ b) ≤ deg(a) and deg(a ∩ b) ≤ deg(b). In particular, deg(a ∩ b) = deg(a) iff a ⊆ b, deg(a ∩ b) = deg(b) iff b ⊆ a, and deg(a ∩ b) = deg(a) = deg(b) iff a ≡ b.
Proof. Let c ≡ a ∩ b. For every x, Wc(x) ≤ Wa(x) and Wc(x) ≤ Wb(x). Summing over x validates the first statement of the theorem. In the second part, deg(a ∩ b) = deg(a) implies that Wc(x) = Wa(x) ∀ x. [The validity of this statement is shown in an exercise.] Then c ≡ a, so a ⊆ b by definition. The converse is proven by noting that a ⊆ b implies that Wa(x) is never greater than Wb(x). Thus by definition Wc(x) = Wa(x) ∀ x, so deg(c) = deg(a).
In general, the degree of the intersection can be interpreted as the amount by which two munbers are equal, but there are problems if the munber is not positively weighted. Most obvious is the possibility that the intersection exists but has degree zero.
| (a) x² - 4x + 4 | (d) x³ - 8x² - 4x - 4 |
| (b) x² - 4x | (e) x6 - 1 |
| (c) x4 + 9x³ - 9x² | (f) x³ - 9x + 3 |
PLEASE SEND ALL TEXT-BASED SENSUALITY TO <GOOBNET@GOOBNET.NET>
© 2018 GOOBNET ENTERPRISES, INC [WHICH DOESN’T ACTUALLY EXIST HOWEVER]
THIS FILE ACCURATE AS OF: THU 06 DEC 2018 – 06:34:49 UTC · GENERATED IN 0.004 SECONDS