 |
 |
 |
 |
 |
 |
| AN ANAGRAM FOR "GOOBNET" IS "GO ON, BET" | |||||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 | |||||||||||
|
|
| |||||||||
| |||||||||||
| |||||||||||
WEEKLY WHINE
Fermat's spiral
Fermat's Spiral is a spiral defined in polar coordinates by r² = a²q. It looks like this.
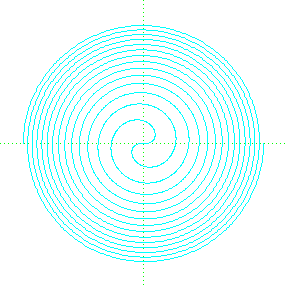
It's an interesting spiral in that it is similar to the Spiral of Archimedes, but not quite. You can get the Spiral of Archimedes by desquarinizing r and a in the above equation. [Actually, you can just desquarinize r, since a is just a constant.] These spirals are both interesting to study, and they have interesting properties.
The History of Mathematics Archive at St Andrews University says that the inverse of Fermat's Spiral is another spiral, defined by inverting theta in the original equation. Its "pedal curve" is almost the same thing.
Fermat's Spiral, in general, hasn't received much attention, mainly because everyone is more concerned with Fermat's Last Theorem, which may or may not be proven depending upon whom you ask. Pierre de Fermat, of course, is known for number theory rather than curves. But he comes from an era when everyone specialized in everything.
If you have a browser that runs Java, you can play with the spiral here, courtesy the aforementioned History of Mathematics Archive at St Andrews. You can get facts about the spiral here.
© 2007 GOOBNET ENTERPRISES, INC [WHICH DOESN'T ACTUALLY EXIST HOWEVER]
THIS FILE ACCURATE AS OF: SAT 17 MAR 2007 – 03:19:46 UTC · GENERATED IN 0.008 SECONDS